Hubbard–Stratonovich transformation

The Hubbard–Stratonovich (HS) transformation is an exact mathematical transformation invented by Russian physicist Ruslan L. Stratonovich and popularized by British physicist John Hubbard. It is used to convert a particle theory into its respective field theory by linearizing the density operator in the many-body interaction term of the Hamiltonian and introducing a scalar auxiliary field. It is defined via the integral identity (Baeurle 2002, Baeurle 2003)

\exp \left\{ - \frac{a}{2} x^2 \right\} = \sqrt{\frac{1}{2 \pi a}} \; \int_{-\infty}^\infty \exp \left[ - \frac{y^2}{2 a} - i x y \right] \, dy,

where the real constant 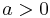a > 0. The basic idea of the HS transformation is to reformulate a system of particles interacting through two-body potentials into a system of independent particles interacting with a fluctuating field. The procedure is widely used in polymer physics (Baeurle 2007, Schmid 1998, Matsen 2002, Fredrickson 2002), classical particle physics (Baeurle 2002a, Baeurle 2004), spin glass theory, and electronic structure theory (Rom 1997, Baer 1998).

Calculation of resulting field theories

The resulting field theories are well-suited for the application of effective approximation techniques, like the mean field approximation (Matsen 2002, Fredrickson 2002) or beyond mean field approximation procedures (Baeurle 2007, Baeurle 2006, Baeurle 2007a). A major difficulty arising in the simulation with such field theories is their highly oscillatory nature in case of strong interactions, which leads to the well-known numerical sign problem (Baeurle 2002, Baeurle 2003). The problem originates from the repulsive part of the interaction potential, which implicates the introduction of the complex factor via the HS transformation. Several analytical and numerical techniques have been developed recently to alleviate the sign problem in Monte Carlo simulation in an efficient way (Baeurle 2002, Baeurle 2002a, Baeurle 2003a).

References

External links